震惊！你知道什么是收敛函数吗？快来一探究竟！
更新时间：2025-05-13 12:35:03
编辑：golfshowsz
来源：网络未知
在数学的浩瀚星空中，收敛函数宛如一颗璀璨而独特的恒星，散发着迷人的光芒，吸引着无数数学爱好者去探索它的奥秘。那么，究竟什么是收敛函数呢？
简单来说，收敛函数描述的是当自变量在某个变化过程中，函数值能够逐渐趋近于一个确定的常数。想象一下，函数就像一个旅行者，随着自变量的不断前行，它的取值不是毫无规律地乱跑，而是稳定地朝着一个目标靠近。
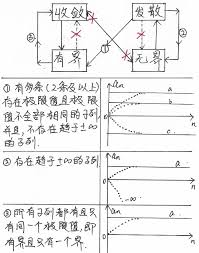
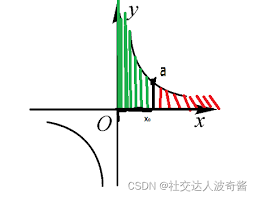
从直观的图像角度来看，如果一个函数的图像在自变量趋近于某个值或者趋于无穷大时，函数曲线能够逐渐逼近一条水平直线，那么这个函数就是收敛的。例如，反比例函数⁄⁄(y=⁄⁄frac{1}{x}⁄⁄)，当⁄⁄(x⁄⁄)趋于正无穷大或者负无穷大时，⁄⁄(y⁄⁄)的值会越来越接近⁄⁄(0⁄⁄)，这就是收敛函数的典型表现。
收敛函数具有许多重要的性质和应用。在理论研究方面，它是分析数学的基石之一，为研究函数的极限、连续性、可微性等提供了关键支撑。在实际应用中，收敛函数更是无处不在。比如在物理学中，许多描述物体运动、变化的规律都可以用收敛函数来刻画，帮助科学家准确预测和理解各种现象。在工程领域，收敛函数用于信号处理、数据分析等，确保系统的稳定性和准确性。
判断一个函数是否收敛，需要运用严谨的数学方法。常见的有极限的定义法、比较判别法、比值判别法等。通过这些方法，我们能够精确地确定函数在特定情况下是否收敛。
收敛函数是数学领域中至关重要的概念，它不仅展现了数学的严谨与美妙，更在众多学科和实际问题中发挥着不可替代的作用。它就像一把神奇的钥匙，打开了一扇扇通往科学真理的大门，引导我们不断深入探索这个充满奥秘的世界。无论是对于专业的数学研究者，还是对数学感兴趣的爱好者来说，深入理解收敛函数都是一次极具价值的数学之旅。
相关文章
更多+
软件合集
更多+
