惊爆!奇函数乘奇函数究竟等于啥?
更新时间:2025-06-05 14:04:03
编辑:golfshowsz
来源:网络未知
奇函数乘奇函数等于什么?这看似简单的问题,实则蕴含着数学世界的奇妙奥秘。
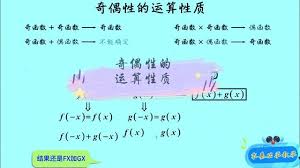
从函数的基本定义出发,奇函数具有 f(-x)= -f(x) 的特性。当我们探讨两个奇函数相乘时,设这两个奇函数分别为 f(x) 和 g(x)。

那么它们的乘积 h(x)=f(x)·g(x)。此时,h(-x)=f(-x)·g(-x)。
因为 f(x) 和 g(x) 都是奇函数,所以 f(-x)= -f(x),g(-x)= -g(x)。
将其代入 h(-x) 的表达式中,可得 h(-x)=[-f(x)]·[-g(x)] = f(x)·g(x) = h(x)。
这一结果表明,两个奇函数相乘得到的函数是偶函数。
这一结论背后有着深刻的数学原理和美妙的逻辑联系。它反映了函数奇偶性之间的一种独特运算规律,如同数学世界中隐藏的密码,揭示了函数性质的内在关联。
从更广泛的角度来看,这种运算规律体现了数学的简洁性与和谐性。它让我们看到,在看似纷繁复杂的函数世界里,存在着简洁而优美的规律。
奇函数乘奇函数等于偶函数这一结论,在数学的各个领域都有着重要的应用。比如在物理学中,许多物理量的变化规律可以用函数来描述,了解函数的奇偶性运算规律有助于我们更深入地理解物理现象的本质。
在数学研究中,这一规律也为我们探索新的数学概念和解决复杂问题提供了有力的工具。它启发我们不断挖掘数学世界的宝藏,去发现更多隐藏在其中的奇妙规律,感受数学的无穷魅力,让我们在数学的海洋中畅游,不断探索未知的领域,领略数学带来的惊喜与感动。
相关文章
更多+